
Learners’ work with the base-ten system is intertwined with their work on counting and cardinality, and with the meanings and properties of addition, subtraction, multiplication, and division. Using only the ten digits 0 through 9, every number can be represented as a string of digits. The base-ten system is an efficient and uniform system for representing all numbers. Although most of the standards organized under this heading involve whole numbers, the domain includes concepts, properties, and representations that extend to other number systems, to measures, and to algebra. The Operations and Algebraic Thinking domain deals with the basic operations, the kinds of quantitative relationships they model, and consequently the kinds of problems they can be used to solve as well as their mathematical properties and relationships. This domain involves important ideas that need to be taught in ways that are interesting and engaging to young students. Addition, subtraction, multiplication, and division grow from these early roots. Learners build on this work to develop strategies to compare two concrete quantities, two number words and two numerals. The Counting and Cardinality domain begins with early rote counting and moves to counting to find how many in one group of objects. The K-5 domains and associated descriptions appear below. In K–8, these groups are called domains and reflect an area of focus for the grade level.

Structure and Content Summary K-5Īn important feature of the New Jersey Student Learning Standards for Mathematics (NJSLS-M) is their organization into groups of related standards. The knowledge and skills students need to be prepared for mathematics in college, career, and life are woven throughout the mathematics standards. As Confrey (2007) points out, developing "sequenced obstacles and challenges for students…absent the insights about meaning that derive from careful study of learning, would be unfortunate and unwise." Therefore, the development of the standards began with research-based learning progressions detailing what is known today about how students' mathematical knowledge, skill, and understanding develop over time. In addition, the "sequence of topics and performances" that is outlined in a body of math standards must respect what is already known about how students learn. They endeavor to follow the design envisioned by William Schmidt and Richard Houang (2002), by not only stressing conceptual understanding of key ideas, but also by continually returning to organizing principles (coherence) such as place value and the laws of arithmetic to structure those ideas.
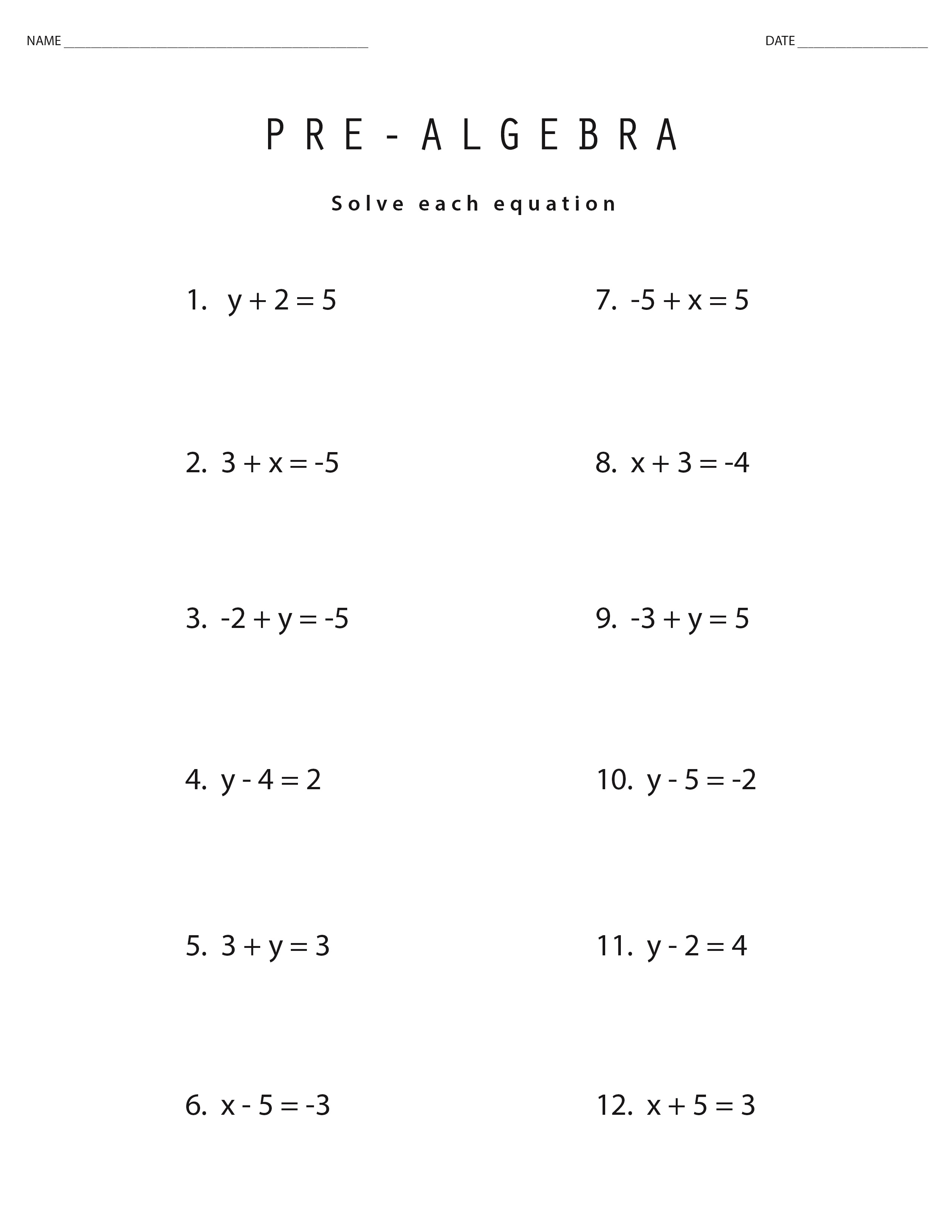
The standards draw on the most important international models for mathematical practice, as well as research. The math standards provide clarity and specificity rather than broad general statements. To deliver on this promise, the 2016 New Jersey Student Learning Standards - Math (NJSLS-M) are designed to address the problem of a curriculum that is "a mile wide and an inch deep."

New Jersey Student Learning Standards for Mathematics Intent and Spiritįor more than a decade, research studies of mathematics education in high-performing countries have concluded that mathematics education in the United States must become substantially more focused and coherent in order to improve mathematics achievement in this country. When properly implemented and coupled with opportunities for students to engage in mathematical investigation, communication and problem solving, rigorous mathematics standards hold the promise of elevating the mathematical knowledge and skill of every learner to levels competitive with the best in the world, of preparing our college entrants to undertake advanced work in the mathematical sciences, and of readying the next generation for the jobs their world will demand.

Successful teaching and learning of mathematics play an important role in ensuring that students have the right skills required to compete in a 21st century global economy.


 0 kommentar(er)
0 kommentar(er)
